Modular Arithmetic

Concepts and Definitions

Modular arithmetic : is a system of arithmetic for integers, which considers the remainder.

Modulo and Modulus : It is basically an operator which is denoted by mod and in programming uses % symbol.

$a \mod N, \ \ a \rightarrow dividend, N \rightarrow divisor \ (Modulus \ | \ Moduli)$

identity element / neutral element : The element of a set of numbers that when combined with another number under a particular binary operation leaves the second number unchanged

$a + 0 = a$

$a \times 1 = a$

inverse element : is another element in the set that, when combined on the right or the left through the binary operation, always gives the identity element as the result.

$a + b = 0 \rightarrow 5 + (-5) = 0$

$a \times b = 1 \rightarrow 5 \times ({1 \over 5}) = 1$

The integers modulo p define a field, denoted by

$F_{p} = \left\{ 0,1,...,p-1 \right\}$

under both addition and multiplication there is an inverse element b for every element a in the set, such that a + b = 0 and a * b = 1.

If the modulus is not prime, the set of integers modulo n define a ring. $F_{n}$

Congruence

Definition by Remainder after Division

$\text{Congruence modulo } m \text{ is defined as the relation } \equiv \ (mod\ m) \text{ on the set of all } a,b \in \mathbb{Z}$

$a \equiv b \ (mod\ m) \ \Longleftrightarrow \ a \mod m = b \mod m$

Definition by Integer Multiple

$\text{We also see that } a \text{ is congruent to } b \text{ modulo } m \text{ if their difference is a multiple of } m$

$a \equiv b \ (mod\ m) \ \Longleftrightarrow \ \exists k \in \mathbb{Z} \ \ : \ \ a - b = km$

$a \equiv b \ (mod\ 0) \ \Longrightarrow \ a \mod 0 = b \mod 0 \ \Longrightarrow \ a = b$

And

$a \equiv b \ (mod\ 0) \ \Longrightarrow \ a - b = k \times 0 \ \Longrightarrow \ a = b$

GCD from Congruence Modulo m

$\text{Let } a,b, \text{ and } m \in \mathbb{Z}$

$a \equiv b \ (mod\ m) \ \Longrightarrow \ \gcd(a, m) = \gcd(b, m)$

$\text{Since } a \equiv b \ (mod\ m) \ \Longrightarrow \ \exists k \in \mathbb{Z} \ \ : \ \ a = b + km$ $\ \Longrightarrow \ a + km \equiv b \ (mod\ m) \$

$\text{Let } N = a \times b \ \text{ and } \ \exists k \in \mathbb{Z}$

$a + kN \equiv a \ (mod\ ab) \ \Longrightarrow \ a + kN \equiv a \ (mod\ N) \ \Longrightarrow \ c \equiv a \ (mod\ N)$

$\text{Since } a \text{ is a factor of } N \text{ then } \ \Longrightarrow \ \gcd(c, N) = a$

Modular arithmetic properties

$(a+b) \mod n = [(a \mod n) + (b \mod n)] \mod n;$
$(a-b) \mod n = [(a \mod n) - (b \mod n)] \mod n;$
$(a\times b) \mod n = [(a \mod n)\times (b \mod n)] \mod n;$
$10^a \mod n = (10 \mod n)^a;$

My property ^^

$k^{e} \times (x^{e_{1}}y^{e_{2}}z^{e_{3}})^{e_{4}} \equiv k \times (xyz)^e \equiv xyz \equiv 0 \ (mod\ xyz);$

Properties of addition

$\text{If} \ a + b = c, \ then \ a \ (mod\ N) + b \ (mod\ N) \equiv c \ (mod\ N);$
$\text{If} \ a \equiv b \ (mod\ N), \ then \ a + k \equiv b + k \ (mod\ N); \ \text{for any integer} \ k$
$\text{If} \ a \equiv b \ (mod\ N) \ and \ c \equiv d \ (mod\ N), then \ a + c \equiv b + d \ (mod\ N);$
$\text{If} \ a \equiv b \ (mod\ N), then -a \equiv -b \ (mod\ N);$

Properties of multiplication

$\text{If} \ a \times b = c, then \ a \ (mod\ N) \times b \ (mod\ N) \equiv c \ (mod\ N);$

$\text{What is} \ (8 \times 16) \ (mod\ 7) ?$

since

$8 \equiv 1 \ (mod\ 7) \ \text{and} \ 16 \equiv 2 \ (mod\ 7)$

we have

$(8 \times 16) \equiv (1 \times 2) \equiv 2 \ (mod\ 7)$

$\text{If} \ a \equiv b \ (mod\ N), then \ ka \equiv kb \ (mod\ N); \ \text{for any integer} \ k$
$\text{If} \ a \equiv b \ (mod\ N), and \ c \equiv d \ (mod\ N)\ , then \ \ ac \equiv bd \ (mod\ N);$

Properties of Exponentiation

$\text{If} \ a \equiv b \ (mod\ N), then \ a^{k} \equiv b^{k} \ (mod\ N); \ \text{for any positive integer} \ k$

$\text{What is} \ 3 ^{16} \ (mod\ 4) \ ?$

we observe that

$3^{2} \equiv 9 \equiv 1 \ (mod\ 4)$

$3^{16} \ (mod\ 4) \equiv (3^{2})^{8} \ (mod\ 4) \equiv (1)^{8} \ (mod\ 4) \equiv 1 \ (mod\ 4)$

Note

The last digit of a number is equivalent to the number taken modulo 10.

Fermat's Little Theorem

knwing that $p$ is a prime number

$a^{p} \equiv a \ (mod \ p)$
$a^{p-1} \equiv 1 \ (mod \ p)$
$a^{-1} \equiv a^{p-2} \ (mod\ p)$

HOW ?

$a^{p-1} \equiv 1 \ (mod\ p)$
$a^{p-1} \times a^{-1} \equiv a^{-1} \ (mod\ p)$
$a^{p-2} \times a \times a^{-1} \equiv a^{-1} \ (mod\ p)$
$a^{p-2} \equiv a^{-1} \ (mod\ p)$
$a^{p-2} \mod p = a^{-1}$

Euler's Phi-Function | Euler's totient Function

$\varphi(1) = 0;$
$\varphi(p) = p-1;\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p \ is \ prime$
$\varphi(m \times n) = \varphi(m) \times \varphi(n); \ \ \ \ \ \ m \ and \ n \ are \ coprimes$
$\varphi(p^e) = p^e - p^{e-1};\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p \ is \ prime$

Euler's Theorem

$a^{\varphi(n)} \equiv 1 \ (mod \ n)$
$a^{k \times \varphi(n) + 1} \equiv a \ (mod \ n)$
$a^{-1} \equiv a^{\varphi(n) - 1} \ (mod\ n)$

Modular Inverse

$\text{A modular inverse of an integer} \ b \ (mod\ n) \ \text{is the integer} \ b^{-1} \text{ such that :}$

$b \times b^{-1} \equiv 1 \ (mod\ n)$

$\text{So for any element} \ g \ \text{in the field} \ F_{p} \ (not \ F_{n}) \ \text{there exists a unique integer } d \ \text{in the field such that}$

$g \times d \equiv 1 \ (mod\ p) \ \ \ \ OR \ \ \ \ g \times d \ mod \ p = 1$

EX1

$\text{What is the inverse element:} \ 3 \times d \equiv 1 \ (mod\ 13) \ ?$

From the third Fermat's Little Theorem

$d \equiv 3^{-1} \equiv 3^{p-2} \ (mod\ p)$
$3^{-1} \equiv 3^{13-2} \ (mod\ 13)$
$3^{-1} \equiv 9 \ (mod\ 13)$

hence

$3 \times 3^{-1} \equiv 1 \ (mod\ 13)$
$3 \times 9 \equiv 1 \ (mod\ 13)$

finally

$d = 9$

EX2

$\text{What is the inverse element:} \ 3 \times d \equiv 1 \ (mod\ 10) \ ?$

Notice that n = 10, which is not a prime number

But since g and n are relatively prime, we will apply the third Euler's Theorem

$d \equiv 3^{-1} \equiv 3^{\varphi(n)-1} \ (mod\ n)$
$3^{-1} \equiv 3^{\varphi(10)-1} \ (mod\ 10)$
$3^{-1} \equiv 3^{3} \ (mod\ 10) \ \ \ \leftarrow \varphi(10) = \varphi(2) \times \varphi(5) = 4$
$3^{-1} \equiv 7 \ (mod\ 10)$

hence

$3 \times 3^{-1} \equiv 1 \ (mod\ 10)$
$3 \times 7 \equiv 1 \ (mod\ 10)$

finally

$d = 7$

from Crypto.Util.number import inverse
inverse(3, 13)

#====================================================
def egcd(a, b):
    if a == 0:
        return b, 0, 1
    else:
        gcd, u, v = egcd(b % a, a)
        return gcd, v - (b // a) * u, u

def modinv(a, n):
    gcd, x, y = egcd(a, n)
    if gcd != 1:
        return None  # modular inverse does not exist
    else:
        return x % n

modinv(3, 13)
  

Quadratic Residue

If q and n are coprime integers, then q is called a quadratic residue modulo n if the following congruence has a solution

$x^{2} \equiv q \ (mod\ n), \ where \ x \in F_{n}$

Likewise, if it has no solution, then it is called a quadratic non-residue modulo n.

So the square root of the Quadratic Residue modulo an integer equal ±x  

And the square root of the None Quadratic Residue modulo an integer does not exist !!

if n is a prime number you will find out that exactly half of the integers between 1 and p−1 are squares mod p, that is, the congruence

$x^{2} \equiv q \ (mod\ p), \ where \ x \in F_{p}$

has a $\frac{p-1}{2}$ solutions

Find ALL quadratic residues mod 5

$0^{2} \ (mod\ 5) = 0 \ \leftarrow q$
$1^{2} \ (mod\ 5) = 1$
$2^{2} \ (mod\ 5) = 4$
$3^{2} \ (mod\ 5) = 4$
$4^{2} \ (mod\ 5) = 1$

So the quadratic residues mod 5 are 1,4 and the non-residues are 2,3

Note

A number that is congruent to 0 mod p is neither a residue nor a non-residue.

Euler's criterion

A number x is square root of q under modulo p if

$x^{2} \equiv q \ (mod\ p)$

Properties of quadratic (non-)residues

$\text{Quadratic Residue} \times \text{Quadratic Residue} = Quadratic Residue$
$\text{Quadratic Residue} \times \text{Quadratic Non-Residue = Quadratic Non-Residue}$
$\text{Quadratic Non-Residue} \times \text{Quadratic Non-Residue = Quadratic Residue}$

an easy way to remember this :

$\text{Quadratic Residue} \leftarrow 1, \ \ \ \text{Quadratic Non-Residue} \leftarrow 0$

Legendre symbol

The Legendre Symbol gives an efficient way to determine whether an integer is a quadratic residue modulo an odd prime p

$\frac{q}{p} \equiv q^{(\frac{p-1}{2})} \ (mod\ p)$

Legendre's Symbol obeys:

$\left\{\frac{q}{p} = 1\right\} \ \text{if} \ q \ \text{is a quadratic residue and} \ q \not\equiv 0 \ (mod\ p)$

$\left\{\frac{q}{p} = -1\right\} \ \text{if} \ q \ \text{is a quadratic non-residue mod p}$

$\left\{\frac{q}{p} = 0\right\} \ \text{if} \ q \equiv 0 \ (mod\ p)$

Which means given any integer a, calculating pow(q, (p-1)//2, p) is enough to determine if q is a quadratic residue.

Tonelli-Shanks algorithm

is a technique for solving for x in a congruence of the form:

$x^{2} \equiv q \ (mod\ p)$

which is also the square root of quadratic residue modulo a prime

sage: from sage.rings.finite_rings.integer_mod import square_root_mod_prime 

sage: q = ... # the Quadratic Residue
sage: p = ... # the modulus

sage: q = Mod(q, p)

sage: square_root_mod_prime(q, p)

Note

Tonelli-Shanks doesn’t work for composite (non-prime) moduli,

The main use-case for this algorithm is finding elliptic curve co-ordinates

Chinese Remainder Theorem (CRT)

gives a unique solution to a set of linear congruences if their moduli are coprime.

$x \equiv a_{1} \mod n_{1}$

$x \equiv a_{2} \mod n_{2}$

$. \ . \ .$

$x \equiv a_{k} \mod n_{k}$

There is a unique solution :

$x \equiv a \mod N, \ where \ N = n_{1} \times n_{2} \times ... \times n_{k}$

Given the following set of linear congruences:

$x \equiv 2 \ (mod\ 5)$
$x \equiv 3 \ (mod\ 11)$
$x \equiv 5 \ (mod\ 17)$

Find the integer a such that

$x \equiv a \ (mod\ 935)$

the Solution

$\text{1. Find} \ N = n_{1} \times n_{2} \times ... \times n_{k}$
$\text{2. Find} \ N_{1} = \frac{N}{n_{1}} \ , \ N_{2} = \frac{N}{n_{2}} \ , \ ... \ , \ N_{k} = \frac{N}{n_{k}}$
$\text{3. Find the multiplicative inverse of} \ N_{1} \ , \ N_{2} \ , \ ... \ , N_{k} \$ $\text{using the corresponding moduli} \ n_{1} \ , \ n_{2} \ , \ ... \ , \ n_{k} \ , \ \$ $\text{call the inverse} \ N_{1}^{-1} \ , \ N_{2}^{-1} \ , \ ... \ , \ N_{k}^{-1}$ $\text{4. } \ x = (a_{1} \times N_{1} \times N_{1}^{-1}) + (a_{2} \times N_{2} \times N_{2}^{-1}) + ... + (a_{k} \times N_{k} \times N_{k}^{-1})$
$x = 872$

sage: CRT_list([2,3,5], [5,11,17])
872

Modular Binomials

Binomials Theorem

$\text{According to the theorem, it is possible to expand any nonnegative integer power of } (x + y) \text{ into a sum of the form }$

$(x + y)^{n} = \sum_{k=0}^{n} \binom{n}{k} x^{n-k} y^{k} = \sum_{k=0}^{n} \binom{n}{k} x^{k} y^{n-k}$

$\text{Knowing that } \binom{n}{k} = \frac{n!}{k! \ (n-k)!}$

$(x+y)^n = \binom{n}{0} x^n y^0 + \binom{n}{1} x^{n-1} y^1 + \binom{n}{2} x^{n-2} y^2 + \cdots + \binom{n}{n-1} x^1 y^{n-1} + \binom{n}{n} x^0 y^n$

$\ (x+y)^n \equiv (x)^{n} + (y)^{n} \ (mod\ m)$

$\text{Let } N = p \times q \ \text{ and }$
$c_{1} \equiv (2p + 3q)^{e_{1}} \ (mod\ N)$
$c_{2} \equiv (5p + 7q)^{e_{2}} \ (mod\ N)$
$\text{Find the values of } p \text{ and } q \text{ knowing everything else !}$

$c_{1} \equiv (2p)^{e_{1}} + (3q)^{e_{1}} \ (mod\ N)$
$c_{2} \equiv (5p)^{e_{2}} + (7q)^{e_{2}} \ (mod\ N)$

Rise both sides of first equation to e2 and the second one to e1

$c_{1}^{e_{2}} \equiv ((2p)^{e_{1}} + (3q)^{e_{1}})^{e_{2}} \ (mod\ N) \ \ \Longrightarrow \ \ c_{1}^{e_{2}} \equiv (2p)^{e_{1} e_{2}} + (3q)^{e_{1} e_{2}} \ (mod\ N)$
$c_{2}^{e_{1}} \equiv ((5p)^{e_{2}} + (7q)^{e_{2}})^{e_{1}} \ (mod\ N) \ \ \Longrightarrow \ \ c_{2}^{e_{1}} \equiv (5p)^{e_{2}e_{1}} + (7q)^{e_{2}e_{1}} \ (mod\ N)$

Multiply both sides of first equation with 2^(-1 * e1 * e2) and the second one with 5^(-1 * e1 * e2)

$(2^{-e_{1}e_{2}}) \times c_{1}^{e_{2}} \equiv (2^{-e_{1}e_{2}}) \times (2p)^{e_{1} e_{2}} + (2^{-e_{1}e_{2}}) \times (3q)^{e_{1} e_{2}} \ (mod\ N) \ \ \Longrightarrow \ \$ $(2^{-e_{1}e_{2}}) \times c_{1}^{e_{2}} \equiv p^{e_{1} e_{2}} + (2^{-e_{1}e_{2}}) \times (3q)^{e_{1} e_{2}} \ (mod\ N)$
$(5^{-e_{1}e_{2}}) \times c_{2}^{e_{1}} \equiv (5^{-e_{1}e_{2}}) \times (5p)^{e_{2}e_{1}} + (5^{-e_{1}e_{2}}) \times (7q)^{e_{2}e_{1}} \ (mod\ N) \ \ \Longrightarrow \ \$ $(5^{-e_{1}e_{2}}) \times c_{2}^{e_{1}} \equiv p^{e_{2}e_{1}} + (5^{-e_{1}e_{2}}) \times (7q)^{e_{2}e_{1}} \ (mod\ N)$

Subtract both equations from each other

$[(2^{-e_{1}e_{2}}) \times c_{1}^{e_{2}}] - [(5^{-e_{1}e_{2}}) \times c_{2}^{e_{1}} ] \equiv 0 \ +$ $\ [(2^{-e_{1}e_{2}}) \times (3q)^{e_{1} e_{2}}] - [(5^{-e_{1}e_{2}}) \times (7q)^{e_{2}e_{1}}] \ (mod\ N)$

we can get the value of the left hand side since all values are known (lets call it X)

$q = \gcd(X, N)$
$p = N / q$

Diffie-Hellman (DH - Exponential Key Exchange Method)

$\text{Every element of a finite field } F_{p} \text{ can be used to make a subgroup } H \text{ under repeated action of multiplication.}$

$\text{In other words, for an element } g : H = \{g, g^{2}, g^{3}, ...\}$

Primitive Elements / Generators

$\text{A primitive element of } F_{p} \text{ is an element whose subgroup } H = F_{p}$

$\text{which means that every element of } F_{p} \text{ can be written as } \rightarrow \ g^{n} \ mod\ p$ $, \ n \in \mathbb{Z}$

$\text{Because of this, primitive elements are sometimes called generators of the finite field}$

There could be more than one primitive element for the finite field, and rather than using a set and checking if every element of Fp has been
generated, we can also rapidly disregard a number from being a generator
by checking if the cycle it generates is smaller in size than p.

If we detect a cycle before p elements, g can't be a generator of Fp.

def is_generator(g, p):
  for n in range(2, p):
    if pow(g, n, p) == g:
      return False
  return True

p = 28151
for g in range(p):
  if is_generator(g, p):
    print(g)
  

sage: GF(28151).primitive_element()
  

DH Protocol/Procedure

Establish a prime number p and some generator of the finite field g
The user then picks a secret integer a (Private Key) , where a < p , then calculates

$X = g^{a} \ mod\ p$

The user will send g, p (Public Key) and X, making it so difficult to calculate a (by taking the discrete logarithm).
The receiver then picks a secret integer b (Private Key) , where b < p , then calculates

$Y = g^{b} \ mod\ p$

Then he will send back Y
Now both sides can generate their shared keys as follows

$K \ = \ X^{b} \ mod\ p \ = \ Y^{a} \ mod\ p \ = \ g^{a \times b} \ mod\ p$

MITA

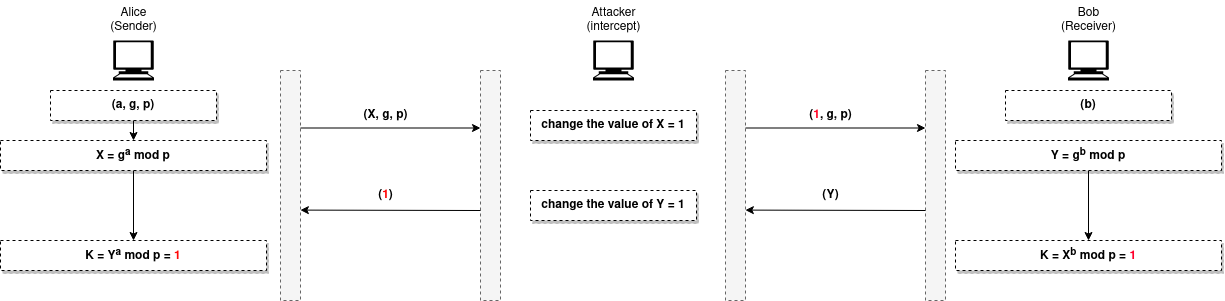
Discrete Log Problem (DLP)

we mentioned that using the primitive element g, every element in Fp can be written as :

$X = g^{n} \ mod\ p$

knowing only the values of X, g, and p leaving as with the problem of finding n, and this is known as the discrete log problem.

$n = log_{g}(X) \ mod\ p$

The discrete logarithm problem is considered to be computationally intractable. That is, no efficient classical algorithm is known for computing discrete logarithms in general.

$\text{all known algorithms run in } O(2^{N^{C}}) \text{ , where } C > 0$

from sympy.ntheory import discrete_log

# A = g^a mod p
a = discrete_log(p, A, g)
  

# A = g^a mod p

# using Pohlig-Hellman and baby-step giant-step alogrithms
sage: a = discrete_log(A, Mod(g, p))

# OR using a Pari znlog (linear sieve index calculus method)
sage: int(pari(f"znlog({int(A)},Mod({int(g)},{int(p)}))"))  # a bit faster 

sage: gp.znlog(A, gp.Mod(g, p))
  

# using sagemath
def pohligHellmanPGH(p,A,g):
    #g must be small
    F=IntegerModRing(p)
    g=F(g)
    A=F(A)
    G=[]
    H=[]
    X=[]
    c=[]
    N=factor(p-1)
    for i in range(0,len(N)):
        G.append(g^((p-1)/(N[i][0]^N[i][1])))
        H.append(A^((p-1)/(N[i][0]^N[i][1])))
        X.append(log(H[i],G[i]))
        c.append((X[i],(N[i][0]^N[i][1])))

    print("G=",G,"\n","H=",H,"\n","X=",X)

    #Using Chinese Remainder
    c.reverse()

    for i in range(len(c)):
        if len(c) < 2:
            break
        t1=c.pop()
        t2=c.pop()
        r=crt(t1[0],t2[0],t1[1],t2[1])
        m=t1[1]*t2[1]
        c.append((r,m))

    print("(a,p-1) =",c[0])
 

sage: a = pohligHellmanPGH(p, A, g)
sage: a 
# G= [8213473543459478292, 3854530033786951538, 15842502293236950997, 11361374755113076881, 4654654383183389733] 
#  H= [7794196832818169365, 1, 12912327280035100030, 14801588540420624265, 15860493449920325450] 
#  X= [3, 0, 83, 1881, 73825648379]
# (a,p-1) = (3466191685115160123, 16007670376277647656)
  

References

https://g.co/kgs/jsEVup
https://cryptohack.org/